本文介绍三篇和图像转换有关的工作，分别是UNIT，MUNIT和CariGANs，解决的是不同domain之间的图像的转换。之前看过的图像转换的工作有CycleGAN、StarGAN等，今天这三篇工作提供了一个新的思路，觉得还蛮有趣的，可能可以将这种方法引入到信息隐藏中来。

UNIT

UNIT（UNsupervised Image-to-image Translation）发表于NIPS2017。UNIT提出了一个称为共享的潜在空间（a shared-latent space）的假设:处于不同domain的两张对应图像可以映射到共享的潜在空间中的同一个潜在表示（latent representation）。基于这个假设，提出了基于GAN和VAE的UNIT框架。

定义$X_1$和$X_2$是两个image domain。在有监督的图像到图像转换中，样本$(x_1, x_2)$服从联合分布$P_{X_1, X_2}(x_1, x_2)$；在无监督的图像到图像转换中，样本$(x_1, x_2)$服从边缘分布$P_{X_1}(x_1)$和$P_{X_2}(x_2)$。没有特殊假设的情况下，我们不能从边缘分布中得出联合分布。

下面给出对共享的潜在空间的假设。如下图所示，给定样本对$x_1$和$x_2$，我们可以从一个潜在编码$z$恢复出这两张图像，也可以从这两张图像得到这个共享的潜在编码。假设存在函数$E_1^*$，$E_2^*$，$G_1^*$和$G_2^*$，满足$z=E_1^*(x_1)=E_2^*(x_2)$。反过来，满足$x_1=G_1^*(z)$和$x_2=G_2^*(z)$。这样以来，$F^*_{1\rightarrow2}(x_1)=x_2=G_2^*(E_1^*(x_1))$实现了从$X_1$到$X_2$的映射，$F^*_{2\rightarrow1}(x_2)=x_1=G_1^*(E_2^*(x_2))$实现了从$X_2$到$X_1$的映射。因此，UNIT要实现的就是$F^*_{1\rightarrow2}$和$F^*_{2\rightarrow1}$。更进一步地，两个函数还满足下面的cycle-consistency constraint：$x_1=F^*_{2\rightarrow1}(F^*_{1\rightarrow2}(x_1))$和$x_2=F^*_{1\rightarrow2}(F^*_{2\rightarrow1}(x_2))$。换句话说，UNIT提出的共享的潜在空间假设满足循环一致性假设（the cycle-consistency assumption）。

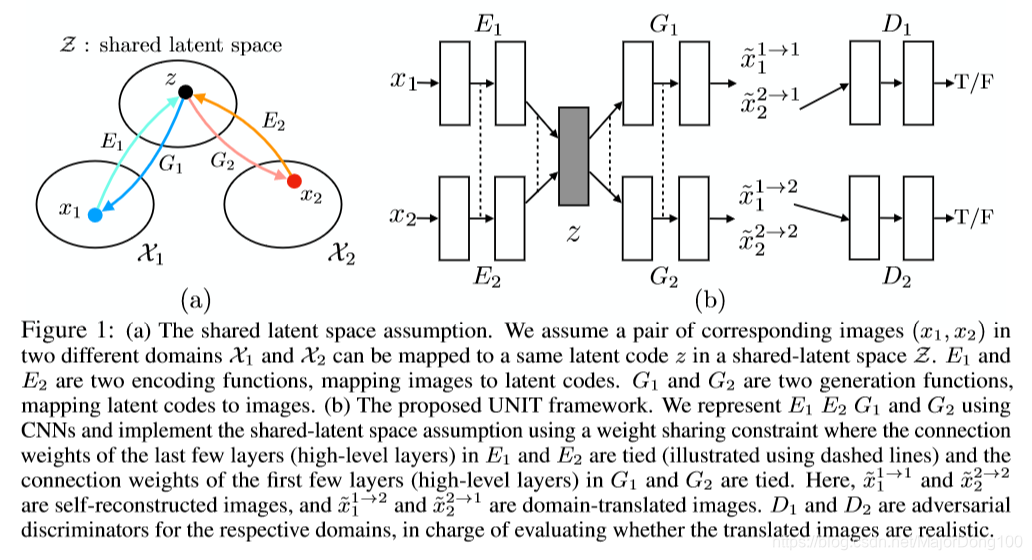
为了实现这样一个共享的潜在空间假设，我们进一步假设一个一个共享的中间表示$h$。这样生成一对对应图像的过程变成了下面这样一种形式：

$$z\rightarrow h^{\nearrow x_1}_{\searrow x_2}$$

因此有了$G_1^*=G_{L,1}^* \circ G_H^*$和$G_2^*=G_{L,2}^*\circ G_H^*$。其中$G_H^*$是一个高阶的生成函数，用来将$z$映射到$h$；$G_{L,1}^*$和$G_{L,2}^*$是低阶的生成函数，用来分别将$h$映射到$x_1$和$x_2$。在多domain的图像转换中，$z$可以表示一个场景的紧凑的、高阶的表示（如车在前，树在后的场景），$h$可以看做是$z$的一个具体的实现（车和树分别占据了对应的像素），而$G_{L,1}^*$和$G_{L,2}^*$则是每个domain中真实图像的生成函数（“tree in lush green in the sunny domain, but dark green in the rainy domain”）。

上图中的框架是基于VAE和GAN的，由六部分组成：两个domain的图像编码器$E_1$和$E_2$，两个domain的图像生成器$G_1$和$G_2$，两个domain的对抗判别器$D_1$和$D_2$。六部分网络的功能可以从下表中看到。

VAE. $E_1$和$G_1$构成了$X_1$ domain的一个变分自编码器$VAE_{1}$。对于一个输入图像$x_1 \in X_1$，$VAE_1$首先通过编码器$E_1$将$x_1$映射到潜在空间$Z$内的一个编码，之后又由生成器$G_1$将这个编码重构成图像$x_1$。另一个变分自编码器$VAE_2$的作用类似。

Weight-sharing. 基于前面介绍的共享的潜在空间假设，我们通过权重共享将两个VAE联系到一起。具体地，我们让$E_1$和$E_2$的最后几层网络共享参数，这几层网络负责从来自两个domain的输入图像中提取到高阶表示。类似地，我们让$G_1$和$G_2$的前几层网络共享参数，这几层网络负责解码高阶表示以重构输入图像。

要注意到权重共享这一约束并不能保证两个domain中的对应图像有着同样的潜在编码。在无监督训练中，在两个domain中不存在成对的对应图像能够映射到同一个潜在编码，即成对的对应图像提取到的签字编码通常是不同的。然而通过对抗训练，我们可以看到来自两个domain的对应图像可以由$E_1$和$E_2$映射到同一个潜在编码，而这个潜在编码又可以由$G_1$和$G_2$分别映射到两个domain中的对应图像。

GANs. 我们的框架中包含了两个生成对抗网络：$GAN_1=\{D_1, G_1\}$和$GAN_2=\{D_2,G_2\}$。在$GAN_1$中，对于第一个domain中的真实图像，$D_1$应该判定为True；对于由$G_1$生成的图像，$D_2$应该判定为False。$G_1$可以生成两种图像：$\tilde{x}_1^{1\rightarrow1}=G_1(z_1 \sim q_1(z_1|x_1))$和$\tilde{x}_2^{2\rightarrow1}=G_1(z_2 \sim q_2(z_2|x_2))$。因为重构的过程是有监督的，我们只能通过对抗训练的方式来实现图像转换的过程。$GAN_2$有着同样的作用。

Cycle-consistency. 由于共享潜在空间假设意味着循环一致性约束，我们还可以在所提出的框架中强制执行循环一致性约束，以进一步规范不适当的无监督图像到图像转换问题。得到的信息处理流称为循环重构流。

Learning. 我们要同时进行$VAE_1$、$VAE_2$、$GAN_1$和$GAN_2$的训练，以同时实现图像重构流、图像转换流和循环重构流：

$$\min_{E_1, E_2, G_1, G_2} \max_{D_1, D_2} L_{VAE_1}(E_1,G_1)+L_{GAN_1}(E_1, G_1, D_1) + L_{CC_1}(E_1, G_1, E_2, G_2) \\ \qquad \qquad \qquad L_{VAE_2}(E_2, G_2)+L_{GAN_2}(E_2, G_2, D_2)+L_{CC_2}(E_2,G_2, E_1, G_1)$$

VAE的训练旨在最小化一个变分的上限（a variational upper bound），VAE的目标是：

$$L_{VAE_1}(E_1, G_1) = \lambda_1 KL(q_1(z_1|x_1)||p_{\eta}(z)) - \lambda_2E_{z_1\sim q_1(z_1|x_1)}[logp_{G_1}(x_1|z_1)]$$ $$L_{VAE_2}(E_2, G_2) = \lambda_1 KL(q_2(z_2|x_2)||p_{\eta}(z)) - \lambda_2E_{z_2\sim q_2(z_2|x_2)}[logp_{G_2}(x_2|z_2)]$$

GAN的目标函数如下：

$$L_{GAN_1}(E_1, G_1, D_1)=\lambda_0E_{x_1\sim P_{X_1}}[logD_1(x_1)] + \lambda_0E_{z_2\sim q_2(z_2|x_2)}[log(1-D_1(G_1(z_2)))]$$ $$L_{GAN_2}(E_2, G_2, D_2)=\lambda_0E_{x_2\sim P_{X_2}}[logD_2(x_2)] + \lambda_0E_{z_1\sim q_1(z_1|x_1)}[log(1-D_2(G_2(z_1)))]$$

我们使用类似于VAE的目标函数来实现循环一致约束：

$$L_{CC_1}(E_1, G_1, E_2, G_2)=\lambda_3KL(q_1(z_1|x_1)||p_{\eta}(z))+\lambda_3KL(q_2(z_2|x_1^{1\rightarrow2})||p_{\eta}(z)) \\ -\lambda_4E_{z_2\sim q_2(z_2|x_1^{1\rightarrow2})}[logp_{G_1}(x_1|z_2)]$$ $$L_{CC_2}(E_2, G_2, E_1, G_1)=\lambda_3KL(q_2(z_2|x_2)||p_{\eta}(z))+\lambda_3KL(q_1(z_1|x_2^{2\rightarrow1})||p_{\eta}(z)) \\ -\lambda_4E_{z_1\sim q_1(z_1|x_2^{2\rightarrow1})}[logp_{G_2}(x_2|z_1)]$$

后面是参数设置与实验过程，这里不再展开。这个工作的一大亮点是在进行两个domain之间的图像转换时引入了一个潜在空间，两个domain内的对应图像会映射到潜在空间中的同一个编码，并通过VAE和GAN实现了这一过程。

MUNIT

Multimodal UNsupervised Image-to-image Translation是ECCV2018的一篇工作，是UNIT思路的一个延续。之前的UNIT实现的是两个domain之间的一个转换，MUNIT更进一步可以实现多个domain之间的转换，下面就来展开介绍这篇论文的细节。

计算机视觉中的很多问题的目标可以理解成是将一个domain中的图像转换到另一个domain，例如超分辨率（super-resolution），着色（colorization），图像修复（inpainting），属性转换（attribute tansfer）和风格迁移（style transfer），因此跨模态的图像转换已经成为了一个研究热点。在很多场景下，跨模态的图像转换的一个重点是多模态（multimodal）的。例如因为天气、时间、光照等的不同，一个冬天的照片转换成夏天的照片可能会是多个样子。但现有的技术通常只能实现某一个模态的转换，这篇论文提出了一个可以实现多模态的无监督图像转换框架。如Fig. 1(a)所示，该框架设定了多个假设。首先，我们假定UNIT中的潜在空间（a latent space）可以解构成一个内容空间（a content space）和一个风格空间（a style space）。进一步地，我们假定来自不同domain的图像可以共享同一个内容空间但不会共享风格空间。为了将一张图像转换到目标domain，我们将这张图像的内容编码（content code）和属于目标domain的一个随机的风格编码（style code）组合到一起就完成了图像的转换（如Fig. 1(b)所示）。也就是说，在做图像转换时，内容编码保留了图像的主要内容信息，这是要保留下来的；而风格编码在转换到下一个domain时是不需要的，因此就扔掉了它。通过抽样几个不同的风格编码，我们就可以产生多样的、多模态的输入样本。（By sampling different style codes, our model is able to produce diverse and multimodal outputs.）多组实验验证了MUNIT的有效性，并达到了state-of-the-art的效果。

定义$x_1\in X_1$和$x_2\in X_2$是来自两个不同domain的图像。在无监督的图像转换任务中，我们可以获得两张图像分别服从的边缘分布$p(x_1)$和$p(x_2)$，但不能获取到联合分布$p(x_1, x_2)$。我们的目标是通过学习到的图像转换模型$p(x_{1\rightarrow 2|x_1})$和$p(x_{2\rightarrow 1|x_2})$来评估两个条件分布$p(x_2|x_1)$和$p(x_1|x_2)$，其中$x_{1\rightarrow 2}$是一个由$x_1$转换到$X_2$的样本。 为了解决这个问题，我们设定了 a partially shared latent space assumption。具体地，我们假定每张图像$x_i\in X_i$是由一个内容潜在编码$c_i\in C_i$和一个风格潜在编码$s_i\in S_i$构成，其中$c_i\in C_i$可以是由两个domain来共享的，而$s_i\in S_i$则是某个domain所特有的。换句话说，服从某个联合分布的一组对应图像$(x_1, x_2)$是由$x_1=G_1^*(c, s_1)$和$x_2=G_2^*(c, s_2)$组成的，其中$c, s_1, s_2$服从某些先验分布，而$G_1^*, G_2^*$是潜在的生成器。更进一步地，我们假定$G_1^*, G_2^*$是目标函数，它们的逆函数为$E_1^*=(G_1^*)^{-1}$和$E_2^*=(G_2^*)^{-1}$。我们的目标就是通过神经网络来学习到这些潜在的生成器和编码器。值得注意的是，尽管编码器和解码器是确定性的，但是由于$s_2$的存在$p(x_2|x_1)$是一个条件分布。 Fig. 2中给出了模型的整体结构和学习过程。一个样本被自动编码器解构成了一个内容编码$c_i$和一个风格编码$s_i$，其中$(c_i, s_i) = (E_i^c (x_i), E_i^s(x_i))=E_i(x_i)$；而图像转换的过程中则用到了“编码器-解码器”对。举例来说，为了将图像$x_1\in X_1$转换到$X_2$，我们首先将图像转换成内容编码$c_1=E_1^c(x_1)$，然后随机选取服从先验分布$q(s_2) \sim N(0, 1)$的风格编码$s_2$。之后使用$G_2$来生成最终的输出图像$x_{1\rightarrow 2}=G_2(c_1, s_2)$。尽管前面这个先验分布不是多模态的，但是因为解码器是非线性的所以输出图像的分布可以是多模态的。

损失函数中包含了一个双向重构损失（a bidirectional reconstruction loss）（保证了编码器和解码器是逆向的）和一个对抗损失（a adversarial loss）（能够让转换得到的图像的分布尽可能地接近目标domain中的图像的分布）。下面具体展开这两部分。

Bidirectional reconstruction loss.

• Image reconstruction

$$L_{recon}^{x_1} = E_{x_1\sim p(x_1)}[||G_1(E_1^c(x_1), E_1^s(x_1)) - x_1||_1]$$ $$L_{recon}^{x_2} = E_{x_2\sim p(x_2)}[||G_2(E_2^c(x_2), E_2^s(x_2)) - x_2||_1]$$

• Latent reconstruction

$$L_{recon}^{c_1}=E_{c_1\sim p(c_1), s_2\sim q(s_2)}[||E_2^c(G_2(c_1, s_2)) - c_1||_1]$$ $$L_{recon}^{s_2}=E_{c_1\sim p(c_1), s_2\sim q(s_2)}[||E_2^s(G_2(c_1, s_2)) - s_2||_1]$$

Adversarial loss.

$$L_{GAN}^{x_2}=E_{c_1\sim p(c_1), s_2\sim q(s_2)}[log(1-D_2(G_2(c_1, s_2)))]+E_{x_2\sim p(x_2)}[logD_2(x_2)]$$

Total loss.

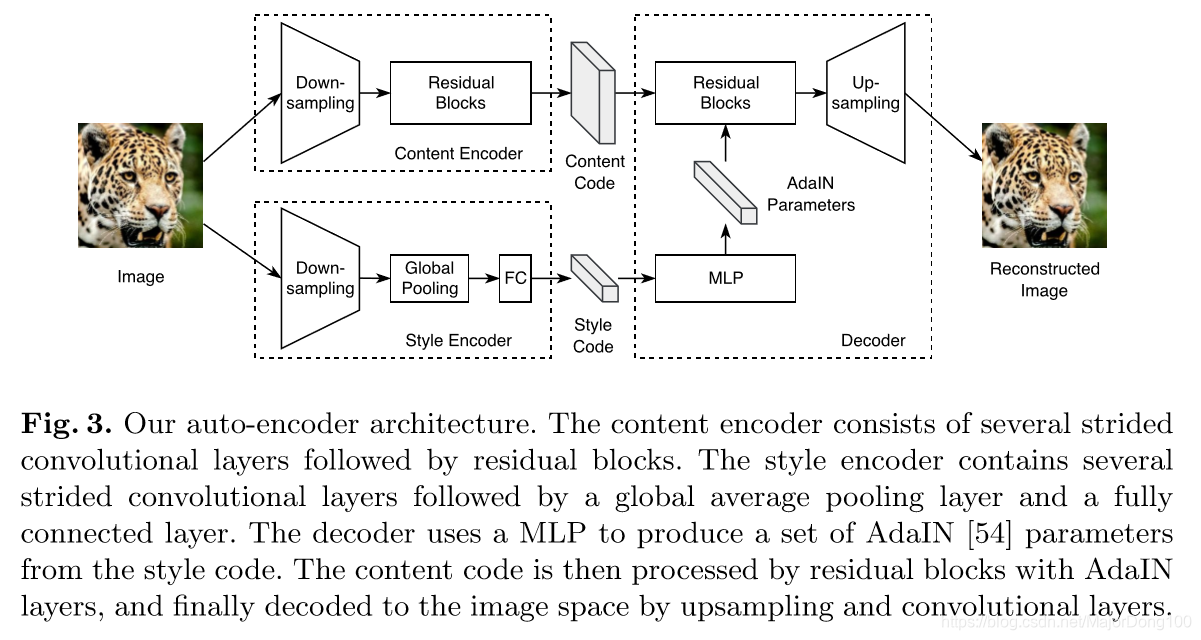
$$\min_{E_1, E_2, G_1, G_2}\max_{D_1, D_2}L(E_1, E_2, G_1, G_2, D_1, D_2) = L_{GAN}^{x_1} + L_{GAN}^{x_2} \\ + \lambda_x(L_{recon}^{x_1}+L_{recon}^{x_2}) + \lambda_c(L_{recon}^{c_1}+L_{recon}^{c_2}) + \lambda_s(L_{recon}^{s_1} + \lambda_{recon}^{s_2})$$

下图是MUNIT的一个具体实现，代码见 https://github.com/nvlabs/MUNIT。